研究概要

量子コンピューティング

研究テーマ

量子コンピュータの応用研究

量子誤り訂正理論

測定型量子計算

量子計算複雑性・量子加速

量子コンピューティング

量子力学は電子や原子などミクロな世界を記述するもっとも基本的な物理法則です。半導体、レーザー、核磁気共鳴、超伝導など、量子力学は縁の下の力持ちとして現代のテクノロジーの基礎を支えています。量子力学は、重ね合わせやエンタングルメントといった日常的な直感から外れた不思議な現象がありますが、これらの性質を計算へと積極的に応用する次世代コンピュータが量子コンピュータです。2014年以降、Google, IBM, Microsoft, Intel, Amazon などといった巨大IT企業が量子コンピュータの開発競争を繰り広げています。2019年には、Googleが開発した量子コンピュータが特定のタスクにおいてスーパーコンピュータよりも圧倒的に高速だったということが話題になりました（参考）。大学や研究所における最先端の基礎研究と大企業やスタートアップにおける応用・開発が互いに蜜に相互作用する科学技術の数少ないフロンティアの一つです。本研究室では、このような量子コンピュータを中心に、量子と情報の融合領域の研究を進めています。2020年からは、文科省Q-LEAP量子AIフラッグシッププロジェクト（代表：藤井）において参加する国内10機関の研究機関を束ねて、日本における量子コンピューティング基礎・応用研究を先導しています。

研究テーマ

藤井研究室では、量子コンピュータや量子情報に関係する、幅広い研究を進めています。ハードウェアに近いところでは、超伝導量子ビット、イオントラップ、量子光学など具体的な物理系のハードウェアのための理論および数値計算、それらを用いた量子コンピュータ・アーキテクチャの設計やハードウェアの制御方法の開発および性能評価、これらアーキテクチャー上で行う量子計算モデルやノイズの問題を克服するための量子誤り訂正法の開発、そして量子コンピュータ上で動作する量子アルゴリズムやさまざまな用途へのアプリケーションの研究を行っています。このように、ハードウェアに近いところからアプリケーションに至るまで一気通貫して１つのグループで研究できることが黎明期である量子コンピュータ研究の面白いところです。また、近年、国内の企業においても量子コンピュータ開発へと舵を切っています。藤井研究室では、これら企業と量子コンピュータの開発及び応用について共同研究を進めています。

量子コンピュータの応用研究

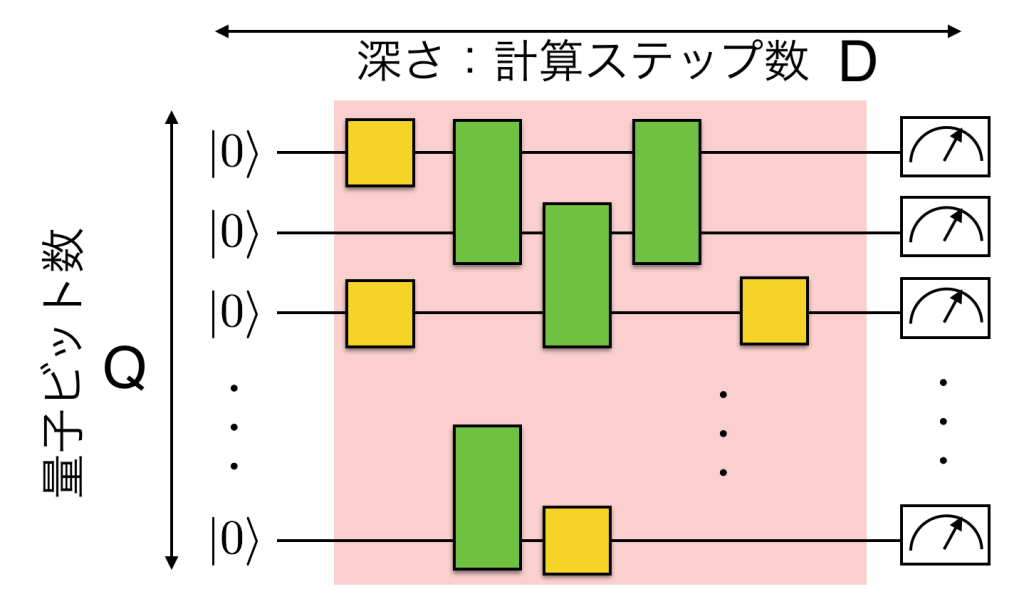
　GoogleやIBM（超伝導量子ビット方式）などの巨大IT企業、そしてIonQ（イオントラップ方式）といったベンチャー企業が、現在数十量子ビット規模の量子コンピュータが提供されている。このような規模の量子コンピュータでは、素因数分解やグローバー探索などの複雑な量子アルゴリズムを動作させることは難しい、一方で、2019年にGoogleが示したように特定のタスクにおいてはスパコンをも上回る計算能力を示す。このようなデバイスはNISQ（noisy intermediate-scale quantum）デバイスと呼ばれており、現在NISQデバイスの活用に向けた研究が世界的に繰り広げられています。当研究室では、NISQデバイスを物性物理や量子化学計算、そして機械学習などへと応用するための研究を進めています。例えば、当研究室から発表した量子回路学習アルゴリズム[1]は、NISQデバイスを用いた世界初の機械学習アルゴリズムとして大きなインパクト与えました（世界TOP 1%論文になっています）。また、この論文は、現在当研究室の助教である御手洗先生が、修士１年生のころに提案したものです。若い人の柔軟でかつ斬新なアイデアが世界を大きく変える可能性のある分野です。Google、オックスフォード大、ロスアラモス研究所など世界の研究者とともに、NISQデバイスのための量子アルゴリズム、変分量子アルゴリズムの解説論文も書いていますのでご参考にしてください[2]。

量子誤り訂正理論

量子状態は環境との相互作用によるデコヒーレンスに弱く安定して量子状態を保持することが難しいという問題があります。また、量子の世界の情報の最小単位である量子ビットは、デジタル化された古典ビット（0,1）とことなり、複素確率振幅というアナログな量によって表現されます。しかも、この複素確率振幅の数（次元）は量子ビットの数に対して指数的増えていきます。これは量子コンピュータの計算能力の源でもあるが、それを精密に制御し、アナログノイズを克服できるかどうか、という問題は量子コンピュータの計算能力を語る上で本質的な問題です。このノイズの問題を克服し、不完全性があるデバイスであっても頑丈な量子コンピュータを作るための理論体系が量子誤り訂正と誤り耐性量子コンピュータです。

量子誤り訂正ではエンタングルした量子状態をうまく利用することによってノイズから量子情報を守ります。環境系とエンタングルしてしまわないように、多数の量子ビットをがっちりをエンタングル（タッグを組ませて）させています。この複雑なエンタングルした状態を記述するために量子多体系のエンタングルメントと幾何学的構造を効率よく記述する枠組みが量子情報分野で構築されてきました。興味深いことに、この枠組みは、物性物理におけるトポロジカル秩序や高エネルギー物理におけるホログラフィック原理の本質をとらえた可解模型として利用されていたり、誤り訂正問題が古典スピングラス模型の相転移問題と密接に関係するなど、物理との接点も与えてくれます。

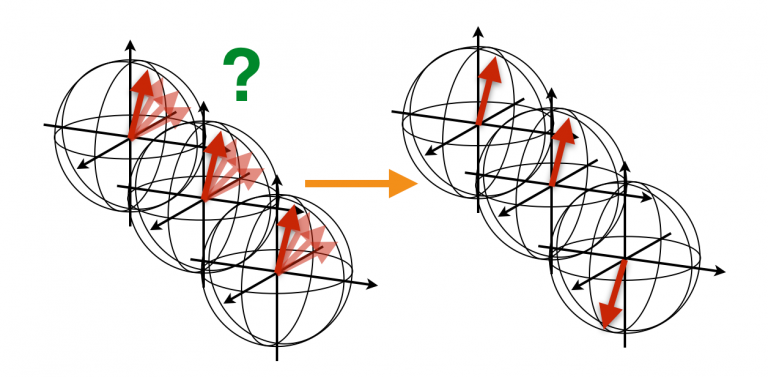
本研究室では、このような量子コンピュータにとって最も重要な技術である量子誤り訂正理論と誤り耐性のある量子コンピュータに関する理論研究を行っています。量子超越性が2019年にgoogleによって示された今、次のマイルストーンは、量子誤り訂正の実現です。googleやIBM、そして国内のプロジェクトにおいても量子誤り訂正の実現にむけて実験が進められています。本研究室では、世界初の量子誤り訂正実証の実現にむけて、新方式の提案や、その理論的解析、数値的な性能評価などで大きく貢献することを目指しています。

測定型量子計算

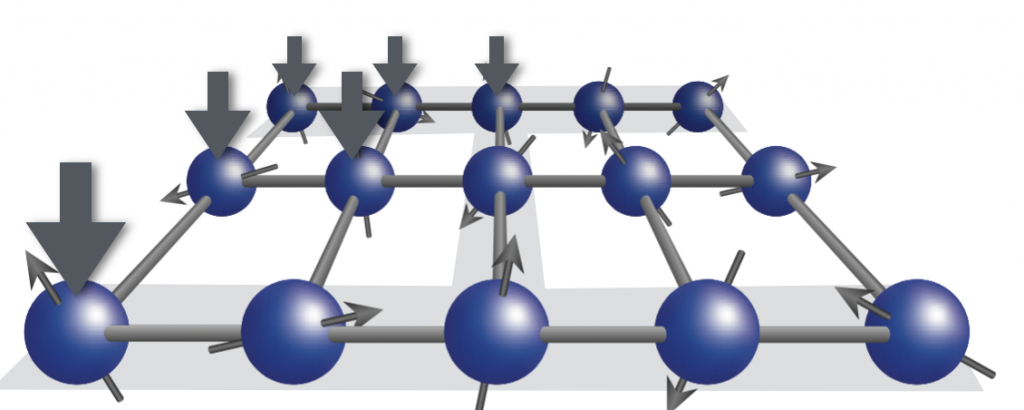
万能な量子計算には、回路型量子計算のほかに測定型量子計算、断熱型量子計算（任意のハミルトニアン）など様々なモデルが知られており、それぞれが互いに等価な計算能力を持つことが知られています。測定型量子計算では、多体エンタングル状態が計算のためのリソースとして与えられ、それに対して測定を行うことによって計算が実行されます。エンタングルしたリソース状態の準備と単一量子ビットの測定という２つのフェイズが切り離されているという特徴があるため、確率的なエンタングル操作しかできないような物理系であっても拡張性のある量子計算が実行できます。また、エンタングルメントの性質などから量子計算能力を議論することもできます。本研究室では、(i)測定型量子計算を用いた誤り耐性量子計算の提案や、(ii)物質系の基底状態や熱平衡状態を測定型量子計算のリソースとして利用する方法、(iii)測定型量子計算の特徴を利用して、メモリーを節約しながら量子計算を古典計算機上でシミュレーションする方法、(iv) リソースとなるエンタングル状態を検証することによる量子計算の検証方法、(v) 測定型量子計算を利用したセキュアクラウド量子計算（ブラインド量子計算）、(vi)測定型量子計算とイジング分配関数との対応、などを研究しています。

量子計算複雑性・量子加速

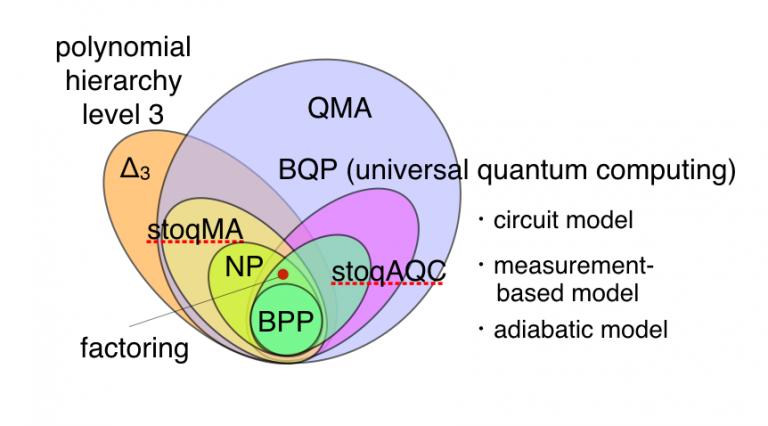
エンタングルメントや局所実在論の否定（ベル不等式の破れ）など、さまざまな観点から量子性（非古典性）が議論されています。量子計算複雑性では、重ね合わせを許す量子力学に基づいた量子コンピュータと従来の古典コンピュータのそれぞれで効率よく解ける問題の違いから、量子と古典の違いに迫ります。一見、量子的に見える物理系であっても、特定の性質を満たせば、古典コンピュータによって効率よくシミュレーションができることも知られています。クリフォード回路、エンタングルメントの少ない量子計算、マッチゲートなどがその例です。これら古典シミュレーション可能なモデルを万能にするために必要な要素から、量子加速に必要な量子性についての定性的および定量的知見を得ることができます。特に、必ずしも万能量子計算に必要な要素を満たさない場合でも、古典コンピュータに対する計算量的な優位性を示す試み（量子超越性）が最近注目を集めています。本研究室では、可換量子回路からなるIQPモデル、1つの純粋量子ビットからなるDQC1モデル、負符号問題が生じないstoquasticハミルトニアンに制限された断熱型量子計算などの準万能量子計算モデルについての研究を行っています。また、古典シミュレーション可能なモデルに対してどのような量子性（マジック状態、ウィグナー関数の負値性、フェルミ粒子の非ガウス状態 etc）を付加することによってどの程度古典シミュレーションが困難になるか定量的なリソース理論の研究も行っています。